No, it is not a typo:
Holo is short for Hologram.
I made up this phrase – (Not-so) Black Holos – as it describes the currently accepted mathematical conception of a Black Hole. (And, no, it does have anything to do with Nail Polish 😏).
The point I am making is that while the physical (macroscopic) object has been around for a while (or so we think), and likely will remain for millions (or billions) of (earth) years, our understanding of what it is has changed (beginning from such a thing cannot possibly exist to yup, it surely exists).
I expect that our conception of “it” will continue to be refined and, probably, even be completely reimagined as we keep thinking about it.
Indeed, as James Jeans wrote in Physics and Philosophy (and he should know! 😏) and I previously quoted him in Deep Beauty?:
The history of theoretical physics is a record of the clothing of mathematical formulae which were right, or very nearly right, with physical interpretations which were often very badly wrong.
This post is triggered by a January 2022 update on Black Hole Information Paradox (BHIP), a topic that I have been casually following — Conspicuous Leisure ☺️ – because I find it exciting and rapid progress is being made (see also the New Horizon Prize 2021):
Snowmass White Paper: Quantum Aspects of Black Holes and the Emergence of Spacetime.
As I had written in Noir Physics, for some time, physicists were working with Thermal (or Classical Thermodynamic) Entropy of Black Holes, and this led to an unsatisfying conclusion that:
Information is lost in a Black Hole.
That is, the radiation that is being emanated by the Black Hole is “random” and it is the same regardless what matter (or photons) entered the Black Hole earlier. This is a violation of a core principle in Quantum Mechanics:
Unitarity.
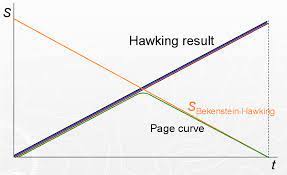
In 1993, Don Page (his 1976 PhD Thesis was co-advised by Kip Thorne and Stephen Hawking), published what is now known as Page Curve, that contrasted fine-grained Entanglement (or von-Neumann, Quantum) Entropy with that of Hawking’s coarse-grained (classical, thermodynamic) one, in:
Information in Black Hole Radiation.
In 1994, Leonard Susskind (building on Stephens, ‘t Hooft and Whiting, Black Hole Evaporation without Information Loss, 1993) wrote:
In 1997, Juan Maldacena’s proposed the duality of Ante-deSitter (AdS) spacetimes and conformal field theories (CFT) in:
The Large N Limit of Superconformal field theories and supergravity.
Looks like the pieces were falling in place:
Entanglement Entropy. Holographic Principle. AdS/CFT correspondence.
In 2006, Ryu and Takayanagi published:
Holographic Derivation of Entanglement Entropy from AdS/CFT.
This appears to have been a tipping point, and with rapid progress (especially from 2014 to 2019), several folks (including those that won the 2021 New Horizons Prize) have more or less cleared up the Black Hole Information Paradox, with one caveat:
We still don’t know very well what is happening inside the Black Hole.
That is:
An observer far away from (and outside!) the Black Hole will not see any contradiction to the Unitary Principle, and will be pleased that Information is not forever lost.
Let me close with a quote from Nette Englehardt (from an interview with Quanta Magazine):
The two papers that kicked this off were work by myself, Ahmed Almheiri, Don Marolf and Henry Maxfield and, in parallel, the second paper, which came out at the same time, by Geoff Penington. We submitted our papers on the same day and coordinated because we knew we were both onto the same thing.
The idea was to calculate the entropy in a different way. This is where Don Page’s calculation was very important for us. If we use Hawking’s method and his assumptions, we get a formula for the entropy which is not consistent with unitarity. Now we want to understand how we could possibly do a calculation that would give us the curve of the entropy that Page proposed, which goes up then comes back down.
And for this we relied on a proposal that Aron Wall and I gave in 2014: the quantum extremal surface proposal, which essentially states that the so called quantum-corrected area of a certain surface inside the black hole is what computes the entropy. We said, maybe that’s a way to do the quantum gravity calculation that gives us a unitary result. And I will say: It was kind of a shot in the dark.
A full resolution of the information paradox would have to tell us exactly how the black hole information comes out. If I’m an observer that’s sitting outside of a black hole and I have extremely sophisticated technology and all the time in the world — a quantum computer taking incredibly sophisticated measurements, all the radiation of that black hole — what does it take for me to actually decode the radiation to reconstruct, for instance, the star that collapsed and formed the black hole? What process do I need to put my quantum computer through? We need to answer that question.
Clearly even the use of “Black” is no longer consistent with this mathematical conception as when Black Hole was coined in the 1960s (as a catchy name to what was previously called Dark Star, by John Michell in 1783, based on escape velocity using Newton‘s Gravitation exceeding the speed of light), it was thought that nothing would be able to come out of it.
Maybe this mathematical conception should be called Holographic Blackish Object: Hobo.😂
PS. No radiation from a real Black Hole has actually been measured yet.






Kool!
nice read