Academic People & Places

The Next Quantum Revolution?

3229 0

Had a great trip to the SF area! The weather was perfect.

After my talk at UC Berkeley (Physics department, in the Center for Quantum Coherent Science‘s conference room) on Thursday, on our first paper, CMU Quantum Group (Raouf, Hedayat and myself) went to Raleigh’s to grab some drinks.

Raleigh’s has a lot of good beer choices. Thankfully, they have some wine choices as well!

We discussed a variety of topics: Quantum Physics, Topos theory….

On Friday, we had a productive day, and an enjoyable Indian lunch, with NASA’s QuAIL group.

Flying back from SF to Pittsburgh, on Saturday, I was happy to read The Second Quantum Revolution in the weekend WSJ by Frank Wilczek, where he writes:

Physicists have learned to use concepts from geometry and topology to understand the enormous complexity that quantum mechanics can generate.

Why was I pleased?

CMU Quantum Group’s second paper employs Morse homology and Gauss-Bonnet theorem — an entirely different approach from mainstream quantum computing research — to study adiabatic quantum computation (AQC).

We hope to shed new light into the very nature of why there could be quantum speedup.

Why take a voyage  — an expedition? — to such exotic places?

Our belief is consistent with that of Richard Feynman in The Character of Physical Law, his Messenger Lecture (in 1964), where he discusses Einstein’s theory:

Newton’s ideas about space and time agreed with experiment very well, but in order to get the correct motion of Mercury, which was a tiny, tiny difference, the difference in the character of the theory was enormous.

The reason is that Newton’s laws were so simple and so perfect, and they produced definite results. In order to get something that would produce a slightly different result it had to be completely different.

In stating a new law you cannot make imperfections on a perfect thing; you have to have another perfect thing.

Roger Penrose — whose Messenger Lecture (in 1990) I attended in person (!) while at Cornell — writes in The Road to Reality:

..the more we probe the fundamentals of physical behavior, the more we find that it is very precisely controlled by mathematics. Moreover, the mathematics that we find is not just of a direct calculation nature; it is of a profoundly sophisticated character, where there is subtlety and beauty not seen in the mathematics that is relevant to physics at a less fundamental level.

….progress, if it is not able to be guided in detail by experiment, must rely more and more heavily on the depth of the mathematics, to “sniff out” the appropriate ideas by use of a profoundly sensitive aesthetic mathematical appreciation.

On the other hand, Richard Mueller (love his books!) writes in Now: The Physics of Time:

Advance is unlikely, in my mind, to require complex math or arcane philosophy. Whoever cracks open these problems will likely do so with very simple examples, maybe using nothing more than algebra.

So? More math or less math?

I think what might work is:

Focus on very simple examples, but study them through profoundly aesthetic mathematics!

So our second paper opens with examining Quantum Search — the simplest example in all things quantum computing — using Morse theory and zooming in to the saddle point using ideas from differential geometry.

Here we go. Ready?

(1)   \begin{equation*} H(s) = (1-s) H_{initial} + sH_{final} \end{equation*}

where s=t/T, T>0, and

(2)   \begin{eqnarray*} H_{initial} &=& 1 - |\hat 0\rangle \langle \hat 0|, \\[3mm] H_{final} &=& \sum_{z\in \{0, 1\}^n - \{ u\} } |z\rangle \langle z| = 1 - |u\rangle \langle u|. \end{eqnarray*}

As usual, the notations \{|z\rangle\}_{z\in \{0, 1\}^n} and \{|\hat z\rangle\}_{z\in \{0, 1\}^n} stand for the computational and Hadamard basis, respectively.

The state |u\rangle is the sought item, the unsorted database being the computational basis \{|z\rangle\}_{z\in \{0, 1\}^n}.

The search problem can be put into the two-dimensional subspace spanned by  |v\rangle := |\hat 0\rangle- 1/\sqrt{N} |u\rangle and |u\rangle.

In this orthogonal basis, the restricted Hamiltonian is

(3)   \begin{equation*} H(s)= \begin{pmatrix} {\frac { \left( 1-s \right) \left( N-1 \right) }{N}}&{\frac { \left( -1+s \right) \left( N-1 \right) }{{N}^ {3/2}}}\\ \noalign{\medskip}{\frac {s-1}{\sqrt {N}}}&{\frac {1-s+sN}{N} } \end{pmatrix}. \end{equation*}

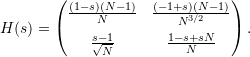
Of course, N=2^n.

The characteristic polynomial of this matrix is

(4)   \begin{equation*} f(s, \lambda) = {\frac { \left( N-1 \right) }{{N}}} (s-s^2) + \lambda^2-\lambda, \end{equation*}

and has one critical point p= (s=1/2, \, \lambda=1/2) obtained by equating its partial derivatives to zero.

This critical point is non degenerate since the eigenvalues {k_1(p) :=2} \, \mbox{ and } k_2(p) := -2\,{\frac { \left( N-1 \right) }{{N}}} of the Hessian of f are non zero, and because k_1(p) k_2(p)<0, the critical point is a saddle point.

Now, the graph of the function f comes with a Gaussian curvature K(s, \lambda)=(f_{ss}f_{\lambda \lambda}-f_{\lambda}^2)/(1+f_s^2+f_\lambda^2)^2.

Gauss-Bonnet theorem forces this curvature to distribute itself on the surface consistently with this topology (consistent with Euler characteristic of -1).

Since the surface has only one critical point, the curvature is concentrated around it.

In fact, the curvature is dumped at the critical point:

(5)   \begin{equation*} \int_{(M, \partial M)} K d\sigma \sim \int_{V(p)} K d\sigma = -2\pi + O(N) \end{equation*}

where V(p) is an arbitrary small neighbourhood around the saddle point p, and independent of n.

This gives the rate at which the curvature is distributed around the saddle point.

Explicitly, we have, K(p)=k_1(p)k_2(p) = -4(1-\frac{1}{N}) and the two quantities k_1(p), k_2(p) are the two principal curvatures of at p.

If we intersect the surface with planes horizontal to the tangent plane T_pM, in particular the plane f(s, \lambda)=0, we obtain two hyperbola called  Dupin indicatrix.

The radius g(s) of this indicatrix (that is, the distance between the two hyperbola), which is also the energy difference, depends on the amount of curvature at p and shrinks exponentially as it gets closer to the tangent plane.

Indeed, we have

(6)   \begin{equation*} g(s) = 2 {\frac {\sqrt {-k_{{2}}(p) \left( 2{ f(p)}+k_{{1}}(p){(s-1/2)}^{2} \right) }}{k _{{2}}(p)}}, \end{equation*}

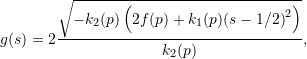
and from which we infer the total time needed to tunnel through p without destroying the adiabaticity as:

(7)   \begin{equation*} \int_0^1 \frac{1}{g(s)^2}ds = {\frac {-k_{{2}}(p)}{\sqrt {k_{{1}}(p) {{ f(p)}}}}} \arctan \left( {\frac {\sqrt {k_{{1}}(p)} }{\sqrt {{ 8 f(p)}}}} \right) \end{equation*}

which can be written as

(8)   \begin{equation*} \frac{\pi}{2} \,\sqrt {N}-1+O \left( {\frac {1}{\sqrt {N}}} \right). \end{equation*}

Our approach thus provides a new derivation for quadratic speedup.

Isn’t this beautiful?

Our second paper is now available here.

 

 

 

Leave a Reply

You might also like